| 問い |
問 題 |
| 1. |
【問題】
次の図形の角アの大きさを求めなさい。
|
1.
(1) |
【問題】
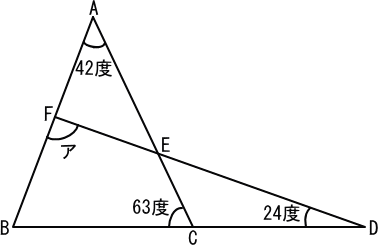
【推理法】
三角形CDEを考えると、
角CEDは、外角の定理より 63−24=39(度)
三角形AEFを考えると、
角AEFは、さっ角により 39(度)
角BFEは、外角の定理より 42+39=81(度)
答 81度
【別解】
三角形ABCを考えると、
180−42−63=75(度)
三角形BDFを考えると、
180−24−75=81(度)
|
1.
(2) |
【問題】
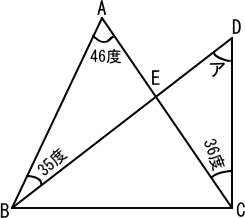
【推理法】
三角形ABEを考えると、
角AEDは、外角の定理により 35+46=81(度)
三角形CDEを考えると、
角CEDは、外角の定理により 81−36=45(度)
答 45度
【別解】
三角形ABEを考えると、
180−46−35=99(度)
三角形CDEを考えると、
180−36−99=45(度)
|
1.
(3) |
【問題】
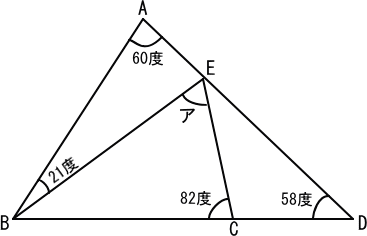
【推理法】
三角形ABEを考えると、
角BEDは、外角の定理により 60+21=81(度)
三角形BDEを考えると、
角DBEは、180−81−58=41(度)
角BECは、180−82−41=57(度)
答 57度
【別解】
三角形ABDを考えると、角ABDは、
180−60−58=62(度)
三角形CDEを考えると、角CBEは、
62−21=41(度)
角BECは、
180−82−41=57(度)
|
| 2. |
【問題】
次の図の直線XとYは平行で、三角形ABCと交わっています。
このとき、角アの大きさを求めなさい。
|
2.
(1) |
【問題】
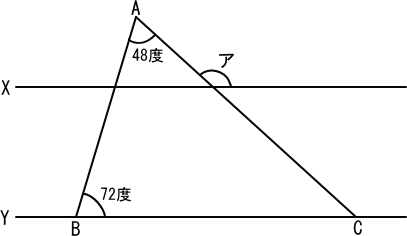
【推理法】
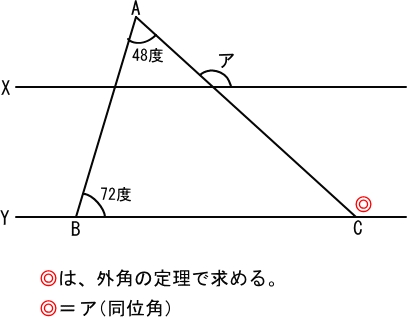
三角形ABCを考えると、角◎は、
48+72=120(度)
同位角により、角アは、120(度) 答 120度
|
2.
(2) |
【問題】
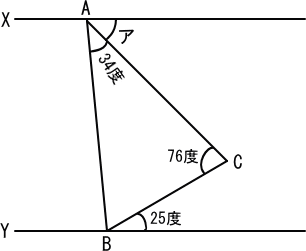
【推理法】
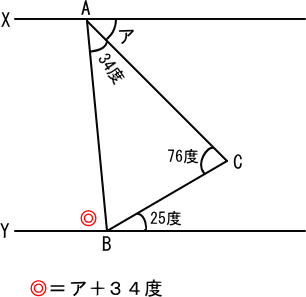
三角形ABCを考えると、角ABCは、
180−34−76=70(度)
角◎は、
180−25−70=85(度)
角◎=34(度)+ア
85−34=51(度) 答 51度
|
| 3. |
【問題】
次の図形の角アの大きさを求めなさい。
|
3.
(1) |
【問題】
下図の四角形ABCDは、長方形です。
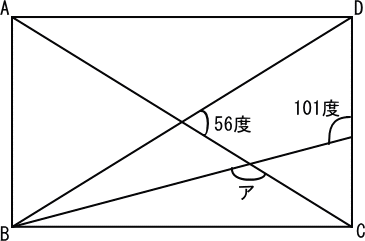
【推理法】
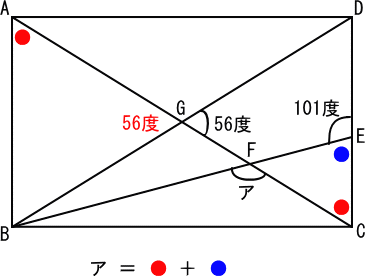
点E,F,Gを定めます。
角AGBは角CGDの対頂角で、56度。
三角形ABGは二等辺三角形だから、角BAGは、
(180−56)÷2=62(度)・・・●
角CEFは、180−101=79(度)・・・●
角ECFは角BAGのさっ角で等しい。
外角の定理により、ア=●+●
ゆえに、
62+79=141(度) 答 141度
|
3.
(2) |
【問題】
下図の四角形ABCDは正方形です。
そして、三角形ADEは正三角形です。
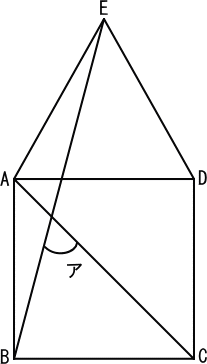
【推理法】
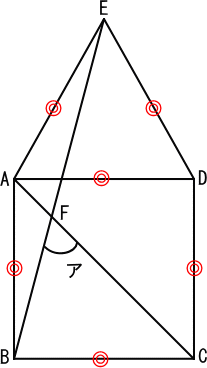
点Fを定めます。
三角形ABEは、二等辺三角形です。
角BAEは、90+60=150(度)
角ABEは、(180−150)÷2=15(度)
角BACは、90÷2=45(度)
三角形ABFを考えると、外角の定理により、
ア=角ABF+角BAF
ゆえに、
15+45=60(度) 答 60度
|
| 4. |
【問題】
AB=BC=CD=DE=EFとなるように、直線AX上に
BとDとFがあり、直線AY上にCとEがあります。
三角形ABCにおいて、角BACが18度のとき、
角DEFの大きさを求めなさい。
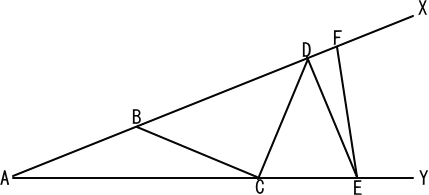
【推理法】
三角形ABC,三角形BCD,三角形CDE,三角形DEF
は、全て二等辺三角形です。
三角形ABCを考えると、角CBDは、外角の定理より、
18×2=36(度)
三角形ACDを考えると、角DCEは、外角の定理より、
18+36=54(度)
三角形ADEを考えると、角EDFは、外角の定理より、
18+54=72(度)
ゆえに、角DEFは、
180−72×2=36(度) 答 36度
【別解】
三角形ABC,三角形BCD,三角形CDE,三角形DEF
は、全て二等辺三角形です。
角CBDは、外角の定理より、18×2=36(度)
角BCDは、180−36×2=108(度)
角DCEは、180−18−108=54(度)
角CDEは、180−54×2=72(度)
角EDFは、180−36−72=72(度)
ゆえに、角DEFは、
180−72×2=36(度)
|
| 5. |
【問題】
下の図の三角形ABCの頂点AからBCに垂直に引いた
直線とBCが交わった点をFとします。
そして、AとFが重なるように折り曲げました。
角EDFが65度のとき、角アと角イの大きさの和を求めなさい。
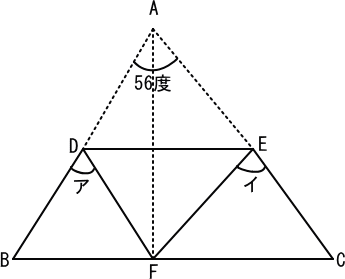
【推理法】
角AEDは、180−(56+65)=59(度)
角ADEと角AEDの大きさの和は、
65+59=124(度)
ゆえに、角BDFと角CEFの大きさの和は、
180×2−124×2=112(度)
答 112度
|
| 6. |
【問題】
下の図形の●ア〜オの角の大きさの和は何度ですか。
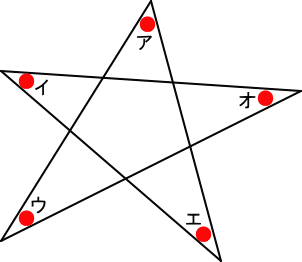
ヒント:『外角の定理』をよく考えて!
【推理法】

外角の定理を考えると、
角アと角ウの大きさの和は、Aと等しくなる。
また、
角イと角エの大きさの和は、Bと等しくなる。
ゆえに、
A+B+オ=180(度)
ア+イ+ウ+エ+オ=180(度) 答 180度

|