図形の扉⑩　　　【正多角形と角度】

　　　　例題
　　　　　　　下の図のように、点Oを中心する円の円周を５等分して、
　　　　　　　正五角形ABCDEを書きました。
　　　　　　　これについて、次の問いに答えなさい。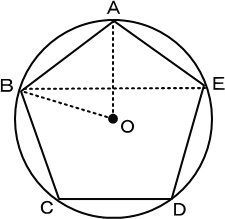
　　　　　　　　　　　　　　　
　　　　　　　（１）角AOBの大きさは何度ですか。
　　　　　　　（２）角BAEの大きさは何度ですか。
　　　　　　　（３）角ABEの大きさは何度ですか。

　　　　　　【円と正多角形を考える】

　　　　　（１）角AOBの大きさは何度ですか。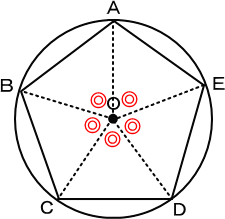
　　　　　　　　　　　　　
　　　　　　　上の図のように、円の中心から円周上のABCDEに直線を引くと、
　　　　　　　等しい大きさの二等辺三角形が５つできます。つまり、角◎が５つ。
　　　　　　　すると、
　　　　　　　角AOB＝３６０÷５＝７２(度)

　　　　（２）角BAEの大きさは何度ですか。

　　　　　　　（１）の図のように、それぞれの三角形は二等辺三角形です。
　　　　　　　三角形ABOで考えると、角AOBが７２度だから、
　　　　　　　角BAO＝(１８０－７２)÷２＝５４(度)
　　　　　　　すると、
　　　　　　　角BAE＝５４×２＝１０８(度)

　　　　（３）角ABEの大きさは何度ですか。
　　　　　　　　　　　　　
　　　　　　　　直線ABと直線AEの長さは等しいから、
　　　　　　　　三角形ABEは、二等辺三角形です。
　　　　　　　　そして、角BAEは１０８度だから、
　　　　　　　　角ABE＝(１８０－１０８)÷２＝３６(度)
「正多角形」の問題は、ウィンベル問題集でしっかり学習しよう！
ウィンベル博士にオンマウス！
　　　　【アドバイス】

　　　「円」と「正多角形」の問題も、
　　　６年生になっても大切な問題だよ！
　　　しっかり覚えておこう！
　　　「辺」と「角度」の関係も大切だよ！

　　※角度の問題は、
　　※「ウィンベル問題集」でしっかり練習だ！