| 栤偄 |
栤丂丂丂戣丂倴倧倢丏侾侾乮曽恮嶼偺悇棟朄乯 |
| 侾丏 |
亂栤戣亃
丂亂摢偺懱憖栤戣亃乮乽堦曕恑傫偩偒傑傝乿乯
丂丂丂摨偠戝偒偝偺敀偲崟偺惓嶰妏宍偺僞僀儖偑偨偔偝傫偁傝傑偡丅
丂丂丂偙傟傪丄壓偺恾偺傛偆偵偁傞偒傑傝偵偟偨偑偭偰側傜傋偰偄偒傑偡丅
丂丂丂偙傟偵偮偄偰丄師偺栤偄偵摎偊側偝偄丅
丂丂丂丂丂丂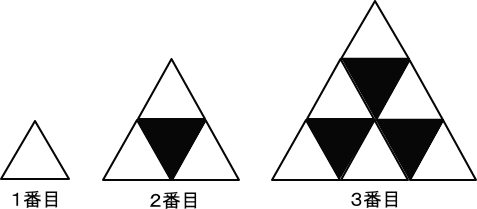
|
侾丏
乮侾乯 |
亂栤戣亃
丂丂丂俆斣栚偺恾宍偵偼丄崟偺僞僀儖偼壗枃巊偄傑偡偐丅
亂悇棟朄亃乮偳傫側偒傑傝偐側丠乯
丂丂丂崟偺僞僀儖傪弴斣偵悇棟偡傞偲丄
丂丂丂侾斣栚佀侽乮枃乯
丂丂丂俀斣栚佀侾乮枃乯
丂丂丂俁斣栚佀侾亄俀亖俁乮枃乯
丂丂丂係斣栚佀侾亄俀亄俁亖俇乮枃乯丂偲側傞丅
丂丂丂偡傞偲丄俆斣栚偺崟僞僀儖偺枃悢偼丄
丂丂丂侾亄俀亄俁亄係亖侾侽乮枃乯丂丂摎偊丂侾侽枃
|
侾丏
乮俀乯 |
亂栤戣亃
丂丂丂俈斣栚偺恾宍偵偼丄敀偺僞僀儖偼壗枃巊偄傑偡偐丅
亂悇棟朄亃乮偳傫側偒傑傝偐側丠乯
丂丂丂乮侾乯偲摨偠傛偆偵丄敀偺僞僀儖傪弴斣偵悇棟偡傞偲丄
丂丂丂侾斣栚佀侾乮枃乯
丂丂丂俀斣栚佀侾亄俀亖俁乮枃乯
丂丂丂俁斣栚佀侾亄俀亖俇乮枃乯
丂丂丂係斣栚佀侾亄俀亄俁亄係亖侾侽乮枃乯丂偲側傞丅
丂丂丂偡傞偲丄俈斣栚偺敀僞僀儖偺枃悢偼丄
丂丂丂侾亄俀亄俁亄係亄俆亄俇亄俈亖俀俉乮枃乯丂丂摎偊丂俀俉枃
|
| 俀丏 |
亂栤戣亃
丂丂丂師偺恾偺傛偆偵丄偛愇傪側傜傋偰拞幚曽恮傪嶌傝傑偟偨丅
丂丂丂偙傟偵偮偄偰丄師偺栤偄偵摎偊側偝偄丅
丂丂丂丂丂丂丂
丂丂丂仸拞幚曽恮乮偪傘偆偠偮傎偆偠傫乯偲偼丄拞傑偱偓偭偟傝偮傑偭偰
丂丂丂仸偄傞曽恮乮惓曽宍偺堄枴偲摨偠乯偺偙偲偱偡丅
|
俀丏
乮侾乯 |
亂栤戣亃
丂丂丂忋偺恾偼丄堦曈偵俈屄偺偛愇偑側傜傫偱偄傑偡丅
丂丂丂偛愇偺悢偼慡晹偱壗屄偱偡偐丅
亂悇棟朄亃
丂丂丂惓曽宍偺柺愊傪媮傔傞偲偒偲摨偠傛偆偵丄
丂丂丂俈亊俈亖係俋(屄)丂丂摎偊丂係俋屄
|
俀丏
乮俀乯 |
亂栤戣亃
丂丂丂忋偺恾偱丄堦斣奜懁偺傂偲傑傢傝偺偛愇偺悢偼壗屄偱偡偐丅
亂悇棟朄亃乮曽恮嶼偺婎慴乯
丂丂丂丂丂丂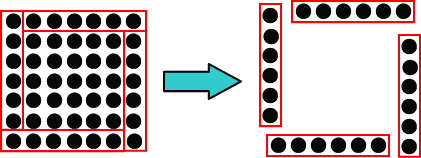
丂丂丂愒慄偱偐偙傫偩俇屄偺偛愇偑係僌儖乕僾偱偒傑偡丅
丂丂丂備偊偵丄傂偲傑傢傝偺偛愇偺悢偼丄
丂丂丂(俈亅侾)亊係亖俀係(屄)丂丂摎偊丂俀係屄
|
俀丏
乮俁乯 |
亂栤戣亃
丂丂丂忋偺恾偺傛偆偵丄慡晹偱俇係屄偺偛愇傪巊偭偰拞幚曽恮傪嶌
丂丂丂傝傑偡丅堦斣奜懁偺傂偲傑傢傝偺偛愇偺悢偼壗屄偱偡偐丅
亂悇棟朄亃
丂丂丂俇係(屄)亖俉(屄)亊俉(屄)丒丒丒丒丒堦曈俉屄偺惓曽宍
丂丂丂偮傑傝丄堦曈俉屄偺拞幚曽恮偑偱偒傑偡丅
丂丂丂偡傞偲丄
丂丂丂(俉亅侾)亊係亖俀俉(屄)丂丂摎偊丂俀俉屄
|
| 俁丏 |
亂栤戣亃
丂丂丂師偺恾偺傛偆偵丄弴斣偵偛愇傪側傜傋偰偄偒傑偡丅
丂丂丂偙傟偵偮偄偰丄師偺栤偄偵摎偊側偝偄丅
丂丂丂丂丂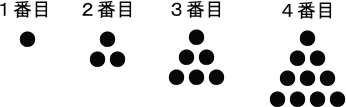
|
俁丏
乮侾乯 |
亂栤戣亃
丂丂丂俉斣栚偺恾偵巊傢傟偰偄傞偛愇偼慡晹偱壗屄偱偡偐丅
亂悇棟朄亃
丂丂丂俉斣栚偺恾偼丄慡晹偱俉抜乮偩傫乯偺惓嶰妏宍偵側傝傑偡丅
丂丂丂偡傞偲丄
丂丂丂丂丂丂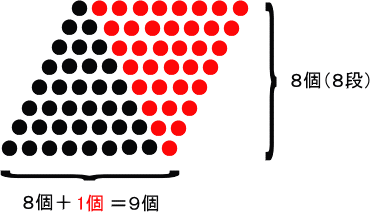
丂丂丂崟偄愇偲愒偄愇傪偁傢偣傞偲暯峴巐曈宍偵側傞丅
丂丂丂暯峴巐曈宍偱峫偊傞偲丄敿暘偺屄悢偵側傞丅丒丒丒丒丒嶰妏宍偺屄悢
丂丂丂戜宍偺柺愊偺媮傔曽偲摨偠偩偭偨偹両
丂丂丂備偊偵丄(忋掙亄壓掙)亊崅偝亐俀亖戜宍偺柺愊
丂丂丂(侾亄俉)亊俉亐俀亖俁俇(屄)丂丂摎偊丂俁俇屄
丂丂丂仸暯峴巐曈宍偱峫偊偰傕戜宍偱峫偊偰傕丄幃偼摨偠偱偡傛丅
|
俁丏
乮俀乯 |
亂栤戣亃
丂丂丂奜懁偺堦曈偑侾侽屄偺偛愇偑側傜傃傑偟偨丅
丂丂丂巊偭偨偛愇偼慡晹偱壗屄偱偡偐丅
亂悇棟朄亃
丂丂丂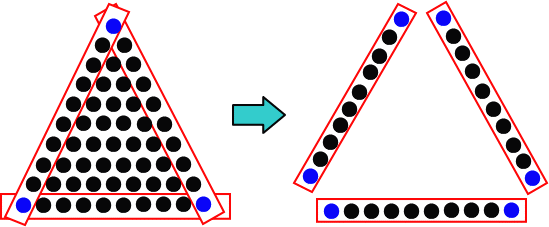
丂丂丂愒慄偱偐偙傫偩侾侽屄偺偛愇偑俁僌儖乕僾偱偒傑偡丅
丂丂丂偡傞偲丄
丂丂丂侾侽亊俁亖俁侽(屄)
丂丂丂偟偐偟丄偙傟偩偲捀揰偺仠傪俀夞寁嶼偡傞偙偲偵側傝傑偡丅
丂丂丂備偊偵丄
丂丂丂俁侽亅俁亖俀俈(屄)丂丂摎偊丂俀俈(屄)
|
俁丏
乮俁乯 |
亂栤戣亃
丂丂丂奜懁偺堦曈偑俇屄偺偛愇傪側傜傋傑偟偨丅
丂丂丂偦偟偰丄偦偺奜懁偺侾傑傢傝偵敀偄偛愇傪側傜傋傑偟偨丅
丂丂丂堦斣奜懁偺敀偄偛愇偼慡晹偱壗屄偱偡偐丅
亂悇棟朄亃
丂丂丂奜懁偺侾傑傢傝偵敀偄偛愇傪側傜傋傞偲丄壓偺恾偺傛偆偵側傝傑偡丅
丂丂丂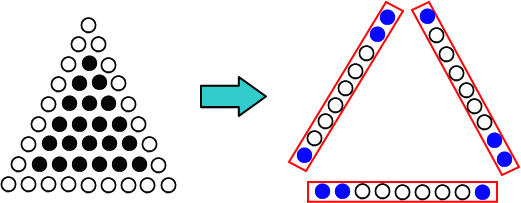
丂丂丂奜懁偺侾傑傢傝偵敀偄偛愇傪側傜傋偨偲偒丄侾曈偺屄悢偼丄
丂丂丂愒慄偱偐偙傫偩俋屄偺偛愇偑俁僌儖乕僾偱偒傑偡丅
丂丂丂偡傞偲丄
丂丂丂俋亊俁亖俀俈(屄)
丂丂丂偟偐偟丄偙傟偩偲捀揰偺仠傪俀夞寁嶼偡傞偙偲偵側傝傑偡丅
丂丂丂備偊偵丄
丂丂丂俀俈亅俁亖俀係屄)丂丂摎偊丂俀係(屄)
丂丂丂亂暿夝亃
丂丂丂俇亄俁亖俋(屄)
丂丂丂(俋亅侾)亊俁亖俀係(屄)丂丂摎偊丂俀係(屄)
|
| 丂丂丂丂丂丂師偺栤戣偼丄偡偙偟擄栤偱偡丅 |
| 係丏 |
亂栤戣亃
丂丂丂壗屄偐偺偛愇傪惓曽宍偵偓偭偟傝側傜傋傑偟偨丅
丂丂丂偡傞偲丄俀侽屄偁傑傝傑偟偨丅
丂丂丂偦偙偱丄奜懁偵侾傑傢傝偛愇傪側傟傋偰憹傗偦偆偲偟偨偲偙傠丄
丂丂丂侾俇屄偨傝傑偣傫偱偟偨丅偛愇偼慡晹偱壗屄偁傝傑偡偐丅
亂悇棟朄亃乮曽恮嶼偺曄壔嘆乯
丂丂丂丂丂丂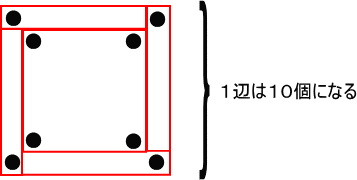
丂丂丂奜懁偺侾傑傢傝偵側傜傋傞偨傔偵昁梫側偛愇偺屄悢偼丄
丂丂丂俀侽亄侾俇亖俁俇(屄)
丂丂丂偡傞偲丄奜懁偺侾曈偺屄悢偼丄
丂丂丂俁俇亐係亄侾亖侾侽(屄)
丂丂丂備偊偵丄慡晹偺偛愇偺悢偼丄
丂丂丂侾侽亊侾侽亅侾俇亖俉係(屄)丂丂摎偊丂俉係屄
|
| 俆丏 |
亂栤戣亃
丂丂丂壗屄偐偺偛愇傪丄傛偙偑偨偰偺俀攞偵側傞傛偆偵側傜傋傑偟偨丅
丂丂丂偡傞偲丄侾俁屄偁傑傝傑偟偨丅
丂丂丂偦偙偱丄奜懁偵侾傑傢傝偛愇傪側傟傋偰憹傗偦偆偲偟偨偲偙傠丄
丂丂丂俋屄偨傝傑偣傫偱偟偨丅偛愇偼慡晹偱壗屄偁傝傑偡偐丅
亂悇棟朄亃乮曽恮嶼偺曄壔嘇乯
丂丂丂丂丂
丂丂丂偨偰偲傛偙偵侾楍偢偮憹傗偡偨傔偵昁梫側偛愇偺悢偼丄
丂丂丂侾俁亄俋亖俀俀(屄)
丂丂丂弶傔偺挿曽宍偺偨偰偲傛偙偵側傜傫偱偄傞悢偺榓偼丄
丂丂丂俀俀亅侾亖俀侾(屄)
丂丂丂偨偰偲傛偙偵側傜傫偱偄傞偛愇偺悢偼丄
丂丂丂俀侾亐(侾亄俀)亊侾亖俈(屄)丒丒丒丒丒偨偰偺悢
丂丂丂俀侾亅俈亖侾係(屄)丒丒丒丒丒傛偙偺悢
丂丂丂備偊偵丄慡晹偺偛愇偺悢偼丄
丂丂丂俈亊侾係亄侾俁亖侾侾侾(屄)丂丂摎偊丂侾侾侾屄
|

