| 問い |
問 題 vol.13(円と正多角形) |
| 1. |
【問題】
次の図形の角★の大きさは何度ですか。求めなさい。
|
1.
(1) |
【問題】
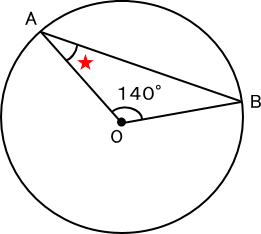
【推理法】
三角形ABOは二等辺三角形だから、角ABOと角BAOは等しい。
ゆえに、
(180−140)÷2=20(度) 答え 20度
|
1.
(2) |
【問題】
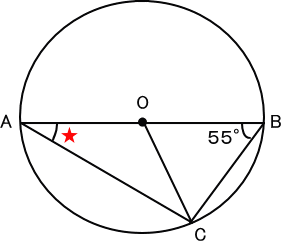
【推理法】
直線BOと直線COは円の半径で長さは等しい。
すると、三角形BCOは二等辺三角形とわかる。
角BOCの角度は、
180−55×2=70(度)・・・・・
角AOCの角度は、
180−70=110(度)
三角形ACOにおいて、
直線AOと直線COは円の半径で長さが等しいので、二等辺三角形。
ゆえに、
(180−110)÷2=35(度) 答え 35度
|
1.
(3) |
【問題】
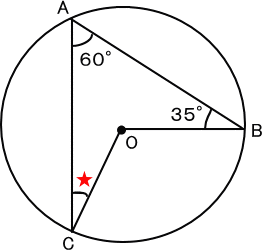
【推理法】
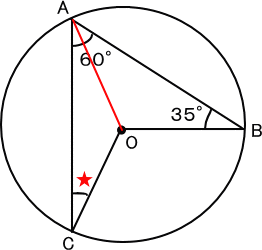
点Aと点Oを結ぶと三角形ABOと三角形ACOができる。
直線AOと直線BOは円の半径で長さが等しいので、二等辺三角形。
すると、角BAOの角度も35度。
三角形ACOにおいて、
直線AOと直線COは円の半径で長さが等しいので、二等辺三角形。
すると、角CAOの角度は、
60−35=25(度)
角CAOと角ACOの角度は等しいので、
ゆえに、答え 25度
|
1.
(4) |
【問題】
図形ABCDEは、正五角形です。
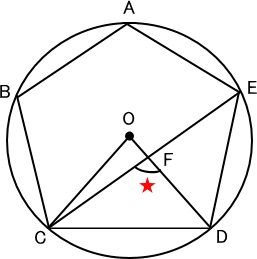
【推理法】
正五角形の性質から、角CODの角度は、
360÷5=72(度)
三角形CDOにおいて、
直線COと直線DOは円の半径で長さが等しいので、二等辺三角形。
すると、角CDOの角度は、
(180−72)÷2=54(度)
正五角形の性質から角CDEの角度は、
54×2=108(度)
三角形CDOにおいて、角DCFの角度は、
(180−108)÷2=36(度)
ゆえに、角CFDの角度は、
180−54−36=90(度) 答え 90度
【外角の定理を利用すると?】
点Eと点Oを結ぶと三角形CEOができる。
正五角形の性質から、角CODの角度は、
360÷5=72(度)
角COEの角度は、
72×2=144(度)
三角形CEOにおいて、
直線COと直線EOは円の半径で長さが等しいので、二等辺三角形。
すると、角FCOの角度は、
(180−144)÷2=18(度)
外角の定理から角CFDの角度は、
180−72−18=90(度) 答え 90度
|
| 2. |
【問題】
下の図のように、直径24㎝と16㎝の2つの円があります。
BはADの3等分の位置にあり、Cは小さい円の中心です。
これについて、次の問いに答えなさい。
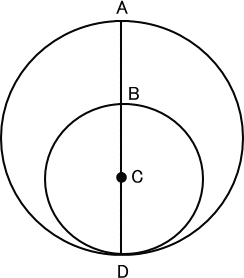
|
2.
(1) |
【問題】
直線BCの長さを求めなさい。
【推理法】
小きい円の半径を求めればよい。
ゆえに、
16÷2=8(㎝) 答え 8㎝
|
2.
(2) |
【問題】
直線ACの長さを求めなさい。
【推理法】
AB=BC=CD
ゆえに、
8×2=16(㎝) 答え 16㎝
|
| 3. |
【問題】
下の正六角形ABCDEFに対角線を全部ひきました。
これについて、次の問いに答えなさい。
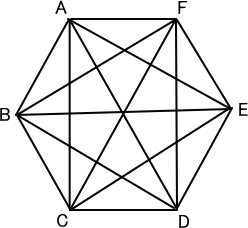
|
3.
(1) |
【問題】
大きさのちがう直角三角形は何種類ありますか。
【推理法】
下の図のように、全部で5種類の直角三角形がある。
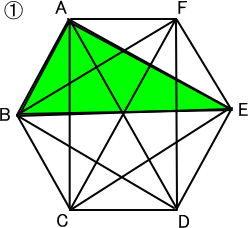 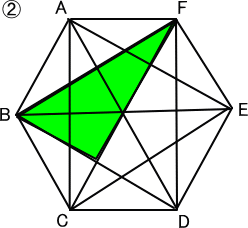
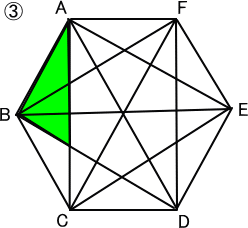 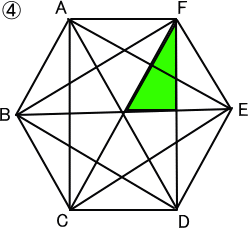
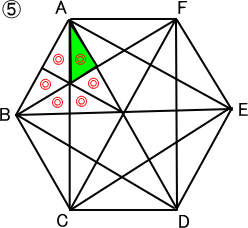
答え 5種類
|
3.
(2) |
【問題】
この正六角形ABCDEFの面積が360c㎡のとき、
(1)の直角三角形のうち、最も小さいものの面積を求めなさい。
【推理法】
正六角形の性質で正三角形が6つできることから、
(1)の⑤の図の通り、
1つの正三角形に6つの二等辺三角形が集まっている。
ゆえに、
360÷6÷6=10(c㎡) 答え 10c㎡
|
3.
(3) |
【問題】
直線ADの長さ20㎝のとき、正六角形のまわりの長さは
何㎝ですか。
【推理法】
正六角形の性質で正三角形が6つできることから、
正三角形のすべての辺の長さは半径に等しいことがわかる。
20÷2=10(㎝)
ゆえに、
10×6=60(㎝) 答え 60㎝
|
3.
(4) |
【問題】
この正六角形ABCDEFの面積は、三角形ABCの何倍
ですか。
【推理法】
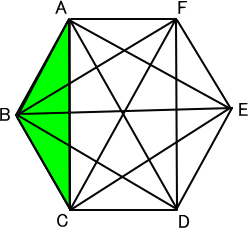
三角形ABCは正三角形1つ分の面積に等しいことがわかるかな?
すると、正六角形の性質で正三角形が6つできることから、
答え 6倍
※正六角形と三角形の関係はわかったかな?
|

