| 問い |
問 題 vol.14(立方体と直方体②) |
| 1. |
【問題】
次の直方体の展開図について、次の問いに答えなさい。
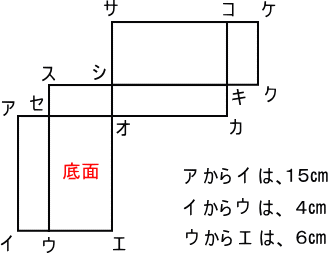
|
1.
(1) |
【問題】
点ウと重なる点はいくつありますか。
【推理法】(展開図折りたたみ法)
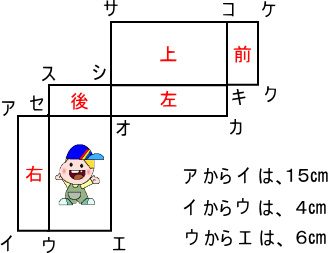
底面に自分が立って、まわりの面を折りたたみます。
すると、右・後・左・上・前の順番で面の位置がわかりますね。
点ウと重なる点は、点ケです。
ゆえに、 答え 1個
|
1.
(2) |
【問題】
辺ウエと重なる辺はどれですか。下の記号から選びなさい。
1、 シス 2、 クケ 3、 サシ
【推理法】
(1)の展開図折りたたみ法で推理すると、
辺ウエと重なる辺は、辺クケになります。
答え 2
|
1.
(3) |
【問題】
この直方体の6面全部の面積は、合計で何c㎡ですか。
【推理法】

辺イウエをよこ、辺アイをたてとした面と面オシスセの和の2倍が全面積となる。
ゆえに、
{(4+6)×15+4×6}×2=(150+24)×2=348(c㎡)
答え 348c㎡
|
| 2. |
【問題】
次の直方体の見取り図と展開図について、次の問いに答えなさい。
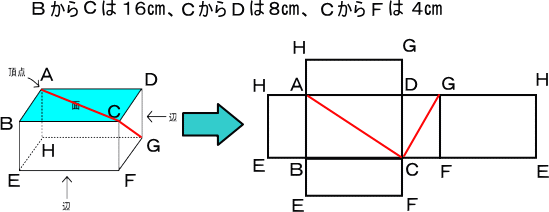
|
2.
(1) |
【問題】
辺HAと辺ADと辺DGと辺GHの長さの和を求めなさい。
【推理法】
辺HAと辺ADの和の2倍が辺HADGHの長さになる。
ゆえに、
(4+16)×2=40(㎝) 答え 40㎝
|
2.
(2) |
【問題】
この直方体の辺の長さの合計は何㎝ですか。
【推理法】
(1)を利用して、
辺HADGHの2倍と辺EHの4倍の和が、この直方体の辺の長さ全部となる。
ゆえに、
40×2+8×4=112(㎝) 答え 112㎝
または、
(16+8+4)×4=112(㎝) 答え 112㎝
|
2.
(3) |
【問題】
三角形ACGの面積を求めなさい。
【推理法】
三角形ACGの底辺の長さは、16+4=20(㎝)
ゆえに、
20×8÷2=80(c㎡) 答え 80c㎡
|
| 3. |
【問題】
下の図は直方体です。この直方体の6つの面の面積の合計が896c㎡のとき、
次の問いに答えなさい。ただし、面BCGFは正方形です。
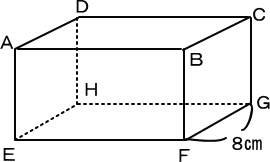
|
3.
(1) |
【問題】
辺ABの長さは何㎝ですか。
【推理法】
この直方体の6つの面の面積の合計を出す式は、
8×8×2+8×AB×4=896(c㎡)
128+32×AB=896(c㎡)
すると、
AB=(896-128)÷32=24(㎝) 答え 24㎝
|
3.
(2) |
【問題】
この直方体の辺の長さの合計は何㎝ですか。
【推理法】
(1)を利用して、
長い辺(24㎝)が4本・短い辺(8㎝)が8本あるので、その和を計算する。
24×4+8×8=160(㎝) 答え 160㎝
|
| 4. |
【問題】
次の立方体の展開図についての質問に答えなさい。
|
4.
(1) |
【問題】
次の展開図を組み立てたとき、側面に「さんすう」とならぶ
ように文字を書きました。文字の向きを考えて「う」はどの
面ですか。なお、答えはカタカナの記号で答えなさい。
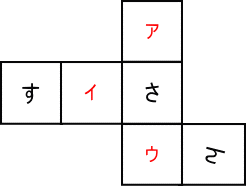
【推理法】
「う」の位置は、以下の通り。
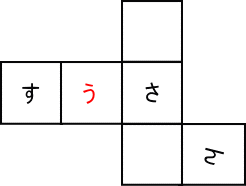
|
4.
(2) |
【問題】
次の展開図を組み立てると、サイコロができます。
アの面の数はいくつですか。
なお、答えは数字で答えなさい。
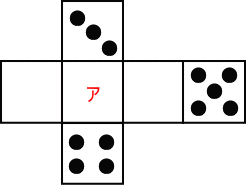
【推理法】
アの面の数は、以下の通り。
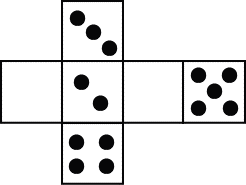
|

