| 問い |
問 題 vol.19(図形問題演習推理法) |
| 1. |
【平面図形の角度問題】
次の図形のアの角度の大きさはそれぞれ何度ですか。
|
1.
(1) |
【問題】
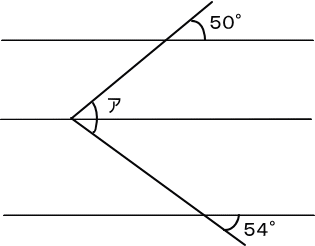
【推理法】(対頂角・同位角)
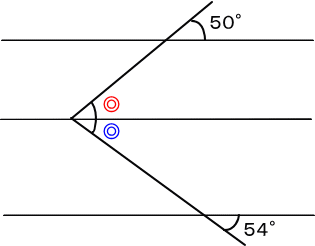
上の図のように、◎と◎の和がアとなる。
すると、
◎と50°、◎と54°はそれぞれ同位角で同じ大きさ。
ゆえに、
50+54=104(度) 答え 104度
|
1.
(2) |
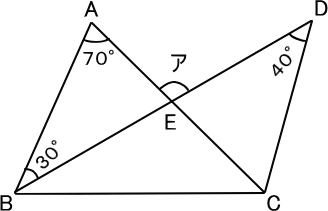
【問題】
【推理法】(外角の定理)
上の図の三角形ABEを考えると、
角AEDは、角ABEと角BAEの和である。
つまり、外角の定理を利用する。
ゆえに、
70+30=100(度) 答え 100度
|
1.
(3) |
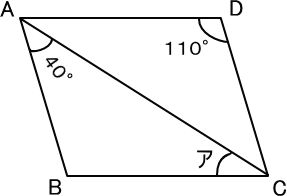
【問題】
四角形ABCDは平行四辺形です。
【推理法】
四角形ABCDは平行四辺形なので、
角ABCは、110度である。
ゆえに、
180-110-40=30(度) 答え 30度
|
1.
(4) |
【問題】
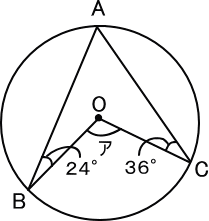
【推理法】
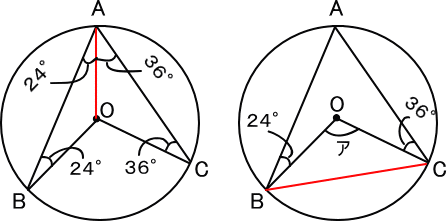
左の図で、三角形ABOと三角形ACOは二等辺三角形。
右の図で、三角形ABCを考えると、
角BACは、24+36=60(度)
180-(角ABC+角ABC)=60(度)だから、
角BOC、つまり角アの角度は、
180-24-36=120(度) 答え 120度
|
1.
(5) |
【問題】
BC=BD、BDとEFは平行です。
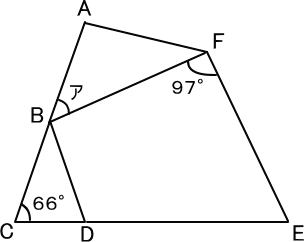
【推理法】
三角形BCDは二等辺三角形で、BDとEFは平行。
すると、角BDC=角DEFは同位角で66度。
角ABDは、外角の定理から、
66+66=132(度)
角BDEは、180-66=114(度)
角DBFは、360-97-66-114=83(度)
ゆえに、
132-83=49(度) 答え 49度
|
| 2. |
【平面図形の面積問題】
次の問いに答えなさい。
|
2.
(1) |
【問題】
次の図形の面積を求めなさい。
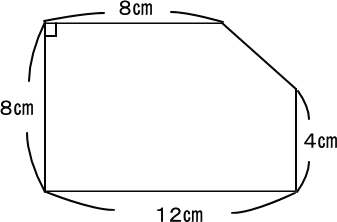
【推理法】(2つの推理法)
【取っちゃえ方式】
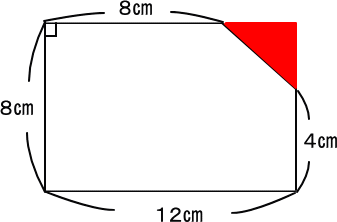
赤色の三角形を取っちゃう方式です。
長方形から赤色の三角形の面積をひく。
ゆえに、
12×8-(12-8)×(8-4)÷2
=96-8=88(c㎡) 答え 88c㎡
【切っちゃえ方式】
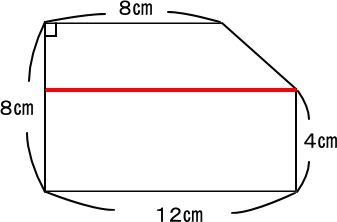
赤線で切っちゃう方式です。
台形と長方形の面積を求めればよい。
台形の面積は、
(8+12)×4÷2=40(c㎡)
長方形の面積は、
4×12=48(c㎡)
ゆえに、
40+48=88(c㎡) 答え 88c㎡
|
2.
(2) |
【問題】
次の図形の面積を求めなさい。
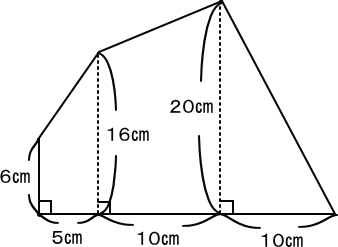
【推理法】
左の台形の面積は、
(6+16)×5÷2=55(c㎡)
まん中の台形の面積は、
(16+20)×10÷2=180(c㎡)
20×10÷2=100(c㎡)
55+180+100=335(c㎡) 答え 335c㎡
|
2.
(3) |
【問題】
次の図の四角形ABCDは、1辺の長さが12㎝の正方形
で、直角三角形ABFと重なっています。
三角形いの面積が三角形あの面積より24c㎡大きい
とき、CFの長さは何㎝になりますか。
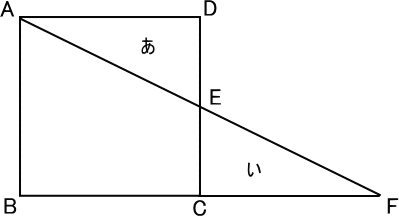
【推理法】
三角形ABFの面積は、四角形ABCDの面積と同じなので、
12×12=144(c㎡)
三角形ABFの面積を考えると、
144-24=120(c㎡)となる。
BFの長さは、
120×2÷12=20(㎝)
CFの長さは、
20-12=8(㎝) 答え 8㎝
|
2.
(4) |
【問題】
次の四角形ABCDは長方形です。
黄色の三角形全部の面積を求めなさい。
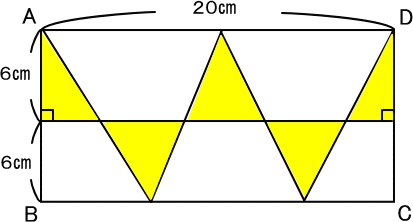
【推理法】(「高さ一定の法則」の利用)
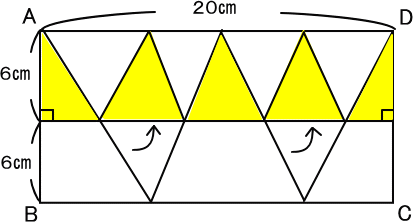
上の図のように、下の2つの三角形を上にあげると、
高さ一定の三角形が5つできます。
すると、
20×6÷2=60(c㎡) 答え 60c㎡
|
2.
(5) |
【問題】
下の直方体の箱を、はば3㎝の赤いテープでまきました。
そして最後に、のりしろ5㎝でつなぎました。
このとき、使ったテープの面積を求めなさい。
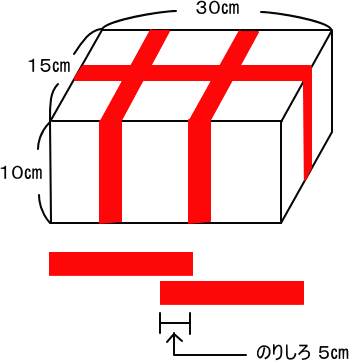
【推理法】
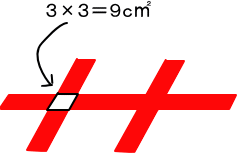
赤いテープでまいたとき、上の図のように重なった部分が4個。
3×3×4=36(c㎡)
そして、のりしろの部分・・・・・3×5=15(c㎡)
30×3×2=180(c㎡)
15×3×4=135(c㎡)
10×3×6=180(c㎡)
180+135+180=495(c㎡)
重なった部分をひくと、
495-36-15=444(c㎡) 答え 444c㎡
|

