【　通過算�C　】

「通過算」の「追いつき追い越し問題」とは、電車などの動く物体が 　　　追いついて・追い越す場合の問題です。 　　「一方を止める」のは、第一変化問題と同じですが、今度は？ 　　速さを飲みこむ物体が逆になる。速さの差を考える問題です。

【例題】　秒速３０ｍの速さで長さ４００ｍの新幹線ひかりが、秒速２０ｍ 　　　　　　の速さで長さ３００ｍの新幹線こだまを追っかけました。 　　　　　　新幹線ひかりが新幹線こだまに追いついて追い越すまでに何秒か 　　　　　　かりましたか。

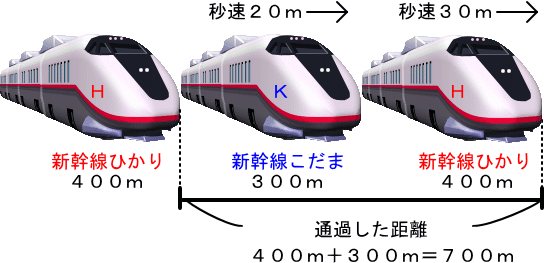【新幹線こだまを止めて考える、しかし？】 　　　 　　　　新幹線こだまを止めて推理します。 　　　　通過した距離は、この２つの新幹線の長さの和です。 　　　　つまり、新幹線こだまのしっぽから新幹線ひかりの頭までの距離です。 　　　　通過距離は、 　　　　４００＋３００＝７００(ｍ) 　　　　しかし、第一変化問題との違いは、次の通り。 　　　　新幹線ひかりの速さは、３０−２０＝１０(ｍ/秒) 　　　　つまり、新幹線ひかりは新幹線こだまに速さを飲みこまれた。 　　　　ゆえに、 　　　　７００÷１０＝７０(秒)　　答　７０秒

ウィンベル博士にオンマウス！

【アドバイス】 　　「追いつき追い越し問題」は、 　動く物体のどちらか一方を止めて考える。 　すると、止めた物体はトンネルや鉄橋と 　同じものと考えれば基本原形２と同じ。 　ただし、速さを飲みこむ物体が逆になる。 　結局、「第一変化問題」「第二変化問題」 　は、「旅人算の出会いと追っかけ」と同じ 　推理法であることがわかりましたか？