「算術ですか?」「おじいちゃん・おばあちゃんの時代の話ですよね。」と、笑われるかもしれません。また、現代ではこの「算術」の言葉自体も死語となっています。
実はこの「算術」が現代社会でも生活の中に根付いています。古来より社会的・経済的なものを背景にして、生産と治水、土地測量、土木事業、堤防、築城、租税などの日常生活に不可欠で、心がけなければいけない修得科目として「算術」は学ばれてきました。
ここで少し「算術の歴史」をご紹介しておきましょう。まずは、古代中国を代表する『九章算術』についてご紹介しましょう。
『九章算術』は、現存する最古の算術書として知られています。また、三世紀半ば頃、「三国志」で有名な魏の国の劉徽(りゅうき)が註釈を行ったことでも有名です。日本では、社会科にも登場する「魏志倭人伝」の卑弥呼の時代のお話です。中国古算書であるこの『九章算術』を解説した大山梅次氏の著書『九章算術について』(平成十五年一月発行・自費出版)によると、「生産と治水、土地測量、面積、体積などの各種計算技能と築城、堤防、土木工事、租税などの日常的内容が含まれている。」と述べられています。そして、「唐宋時代には算学の教科書に使われています。」とも述べられています。
それでは、少し『九章算術』の世界を覗いてみましょう。
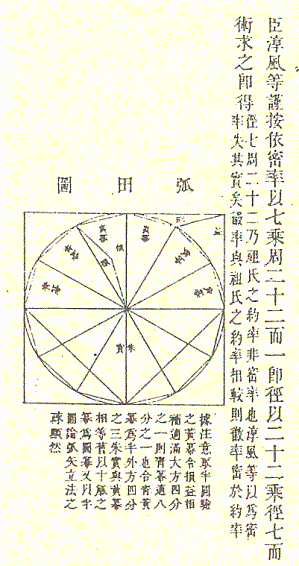
右の図は、大山梅次氏の著書『九章算術について』に掲載されている「田」の面積を求める問題を提示している図ですが、『九章算術』では土地のことを「田」と呼んでいます。土地の形が円の土地についての計算をしている箇所です。
円の面積といえば、この時代の「円周率」の求め方が興味あるところですが、特に、劉徽が註釈をつけた箇所は、「3つの円周率」の考え方の違いを指摘していて、大変興味深い内容が提示されています。「3つの円周率」とは、「3」「3.14」「7分の22」のことです。
まず、劉徽は当時定説となっていた円周率が「3」であることに言及し、円周率が「3」であるときは、円に内接する正六角形の辺の和が直径の3倍となる(これを、「周三径一」という。)ことから正しい値ではないと説明し、内接正六角形の辺を2倍にし、さらに順次倍にしていき、正九十六角形に至り、その周を計算して、「五十分の百五十七」とする(これを、「徽率」という。)と説明しました。この「五十分の百五十七」がまさに「3.14」です。
もう一つの「7分の22」の円周率は、「密率」といい唐の李淳風の円周率です。
実に不思議なことですが、現代の中学入試の問題に登場する円周率が、この「3」「3.14」「7分の22」の3種類なのです。
『九章算術』の形式は、はじめに【問題】があり、次に【答】、そして解き方を示す【術】が続きます。この形式が日本に伝わり、後述の「和算」の形態となっていることは一般にはあまり知られていません。それもそのはずで、この「和算」の「算術」は、日本独特の発達を遂げ、『九章算術』の形式は踏襲していますが、全く別物のような「算術」に変貌しています。
この「和算」は、江戸時代に最高潮を迎えた日本独特の計算芸術として、滑稽本で有名な十辺舎一九の「東海道中膝栗毛」や浮世草子で有名な井原西鶴の「好色一代男」なども及ばない部数が出版され、庶民の間に流布しました。
「和算」の大御所であり、江戸時代のベストセラーといえば、往来物『塵劫記(じんこうき)』(吉田光由著)が有名ですが、吉田光由は社会科の教科書に登場している関孝和(日本の「算聖」とも呼ばれています。)に大きな影響を与えた人です。江戸の庶民たちは、この「算術」を楽しみながら学んだのです。そして、当時の世界水準に引けを取らない高度な智恵を磨いていたのです。往来物とは、主に寺子屋で使用した「初等教育用教科書」の総称です。江戸時代には、社会科にも登場する「御成敗式目」などの法令集も「往来物」と呼んでいたようです。
『関孝和のお墓』←東京の名所の一つです。まさしく、江戸の庶民たち(商人を中心に)は、「生きるための算術」を学んでいたのです。そして、問題の解法が数学の発達に大きな貢献をするのは、現代でもかわりませんが、寺子屋に通うことのできない庶民や、『塵劫記』などの「往来物」も購入することのできない庶民は、どこで勉強したか?
実は、当時の子どもたちは神社仏閣の境内に侵入し、絵馬をまねた「算額」(さんがく)なる板を教科書にして、この算術を学んだのです。前述の関孝和なども、この「算額」を見学しながら算術を学んだのです。そして、現在でも全国各所に「算額」は現存し、「算額」の研究者も存在します。
『和算の館』←「算額」の世界にジャンプします。
このような土壌があったからこそ、日本の明治時代に諸外国から「西洋数学のシステム」がどっと押し寄せてきたときにも、混乱なく、この「西洋数学のシステム」を庶民たちは吸収できたのだと思います。