【問題】　　右下の図のように、正五角形と正八角形が重ねられています。 　　　　　　　　　　　（１）　角Xの大きさを求めなさい。 　　　　　　　　　　　（２）　角Yの大きさを求めなさい。 　　　　　　　　　　　（３）　角Zの大きさを求めなさい。

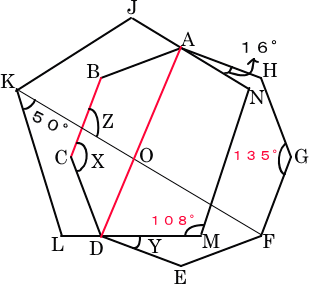（１）　角Xの大きさを求めなさい。 　　　　　　　　　　　　　　　正八角形の内角の和は、１８０×（８−２）＝１０８０（度）である。 　　　　　　　　　　　　　　　角Xの大きさは、１０８０÷８＝１３５（度）となる。 　　　　　　　　　　　（２）　角Yの大きさを求めなさい。 　　　　　　　　　　　　　　　上図の直線ADの補助線を引きます。 　　　　　　　　　　　　　　　正五角形の内角の和は、１８０×（５−２）＝５４０（度）である。 　　　　　　　　　　　　　　　そして、正五角形の１つの内角は、５４０÷５＝１０８（度）である。 　　　　　　　　　　　　　　　上図の補助線ADとAH，DEはそれぞれ垂直になっているので、 　　　　　　　　　　　　　　　角NADは、９０−１６＝７４（度）となり、 　　　　　　　　　　　　　　　四角形ADMNにおいて、 　　　　　　　　　　　　　　　角ADMは、３６０−（７４＋１０８×２）＝７０（度） 　　　　　　　　　　　　　　　ゆえに、角Yの大きさは、９０−７０＝２０（度）となる。 　　　　　　　　　　　（３）　角Zの大きさを求めなさい。 　　　　　　　　　　　　　　　上図の補助線ADと直線KFとが交わった点をOとします。 　　　　　　　　　　　　　　　四角形KLDOにおいて、角LDOは、１８０−７０＝１１０（度）となり、 　　　　　　　　　　　　　　　角KODは、３６０−（５０＋１０８＋１１０）＝９２（度）となる。 　　　　　　　　　　　　　　　補助線ADと直線BCは平行なので、角KODと角Zは、さっ角で同じ大きさ。 　　　　　　　　　　　　　　　ゆえに、角Zの大きさは、９２（度）である。