【全体展望】　この問題は、「時計算」の典型的問題です。「時計算」は角度問題を極めるためには 　　【全体展望】　最良の問題です。ちなみに、長針は１分間に６度、短針は１分間に０．５度回ります。 　　【全体展望】　「時計算の基礎」は、以下のアイコンをクリックしてください。 　　　　　　　　　　　　　　　　　　　　　　　　 　　　【問題】　　太郎君が夕方出かけるときに時計を見たら４時３５分から４時４０分の間をさしていました。 　　　【問題】　　３時間以内に帰って来たら長針の位置と短針の位置が出かけたときとちょうど入れかわっ 　　　【問題】　　ていました。このとき、次の問いに答えなさい。答は整数または分数で答えなさい。

【問題】（１）　外出中に長針の回った角度と短針の回った角度の和を求めなさい。 　　　　【推理法】　問題文の「長針の位置と短針の位置が出かけたときとちょうど入れかわっていました。」とは、 　　　　　　　　　　　下の図１から図２になったということです。帰宅時刻は７時２０分から７時２５分の間。 　　　　　　　　　　　長針と短針がつくる角を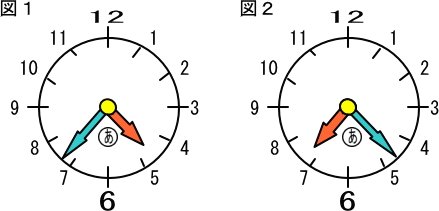とします。 　　　　　　　　　　　　 　　　　　　　　　　　図２（帰宅時刻）について考えると、長針をあと度進めれば、 　　　　　　　　　　　３６０×３＝１０８０（度）回転したことになります。 　　　　　　　　　　　また、外出中に長針が回転した角度は、１８００−（度）となります。 　　　　　　　　　　　そして、外出中に短針が回転した角度は、（度）となりますから、 　　　　　　　　　　　（１０８０−）＋＝１０８０（度）　　　　　　　　　　　　答　１０８０度　 　　　　【問題】（２）　外出中に短針の回った角度を求めなさい。 　　　　【推理法】　「時計算の基礎」です。長針は１分間に６度、短針は１分間に０．５度回転します。 　　　　　　　　　　　３６０÷６０＝６（度）・・・長針は１分間に６度回転します。 　　　　　　　　　　　３０÷６０＝０．５（度）・・・短針は１分間に０．５度回転します。 　　　　　　　　　　　長針と短針が回転した角度の和は、６＋０．５＝６．５（度） 　　　　　　　　　　　時計が回りはじめて１０８０（度）になるのは、 　　　　　　　　　　　　進んで１０８０度となります。 　　　　　　　　　　　ゆえに、外出中に短針が回転した角度は、 　　　　　　　　　　　 　　　　【問題】（３）　帰宅時刻は７時何分ですか。 　　　　【推理法】　まず、７時何００分を考えると、長針と短針のつくる大きい方の角度は、 　　　　　　　　　　　３０×７＝２１０（度） 　　　　　　　　　　　長針は１分間に６−０．５＝５．５（度）ずつ短針に接近する。 　　　　　　　　　　　それでは、長針と短針がつくる角度が（２）になるには、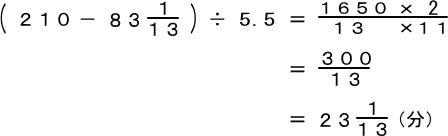