【　図形の周期算　】

図形の周期算は、こんな時に活用します。

例題 　　　　１本のはり金を２�pごとに直角に折り曲げて、下の図のような形を作りました。 　　　　このとき、できた図形グループに順番に番号をつけると最後が�Gになりました。 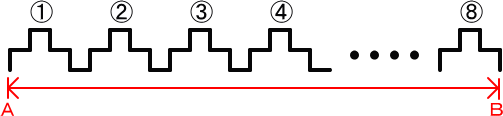　　　　　　　 　　　　（１）AからBまでの長さは何�pですか。 　　　　（２）このはり金の長さは全部で何�pでしたか。 　　　　ただし（１）（２）は、はり金の太さは考えないものとします。

グループ（周期）の２つの推理法 　　　　　（１）グループ（周期）は、２種類考えることができます。 　　　　　　　　�@はんぱを考える 　　　　　　　　　　 　　　　　　　　　　周期の長さは、２×４＝８�p 　　　　　　　　　　はんぱの長さは、２×３＝６�p 　　　　　　　　　　ゆえに、 　　　　　　　　　　８×（８−１）＋６＝６２(�p) 　　　　　　　　�A植木算方式で考える 　　　　　　　　　　 　　　　　　　　　　周期の長さは、２×３＝６�p　　６×８＝４８(�p) 　　　　　　　　　　間の長さは、２�p　　　　　　　　　　　２×（８−１）＝１４(�p) 　　　　　　　　　　ゆえに、 　　　　　　　　　　４８＋１４＝６２(�p) 　　　　　（２）グループ（周期）は、２種類考えることができます。 　　　　　　　　�@はんぱを考える 　　　　　　　　　　 　　　　　　　　　　周期の長さは、２×８＝１６�p 　　　　　　　　　　はんぱの長さは、２×７＝１４�p 　　　　　　　　　　ゆえに、 　　　　　　　　　　１６×（８−１）＋１４＝１２６(�p) 　　　　　　　　�A植木算方式で考える 　　　　　　　　　　 　　　　　　　　　　周期の長さは、２×７＝１４�p　　１４×８＝１１２(�p) 　　　　　　　　　　間の長さは、２�p　　　　　　　　　　　　　２×（８−１）＝１４(�p) 　　　　　　　　　　ゆえに、 　　　　　　　　　　１１２＋１４＝１２６(�p)

ウィンベル博士にオンマウス！

【アドバイス】 　　　「図形の周期算」は、 　　　「はんぱを考える」「植木算方式を考える」 　　　の２種類の推理法があるんだよ！ 　　　周期の形に気をつけて、 　　　周期がわかれば、何番目でもだいじょうぶ！ 　　　植木算の復習は、以下の通り。 　　　植木算の応用�@の復習 　　　植木算の応用�Aの復習